The straight line method is the easiest way of spreading the cost of an asset over its useful life.
In this lesson, I explain the basics of straight line method and how you can use it to calculate the depreciation expense.
Straight Line Depreciation
The Straight Line Method charges the depreciable cost (cost minus salvage value) of a long-term asset to the income statement equally over its useful life.
For example, a machine that costs $110,000 with a useful life of 10 years and salvage value of $10,000 will be depreciated by $10,000 each year [(110,000 – 10,000) ÷ 10].
Under the straight line method, the depreciation expense is evenly distributed over the asset’s life.
If we plot the depreciation expense of an asset with a depreciable cost of $5000 and 5 years of useful life using the straight line method, it will look something like this:
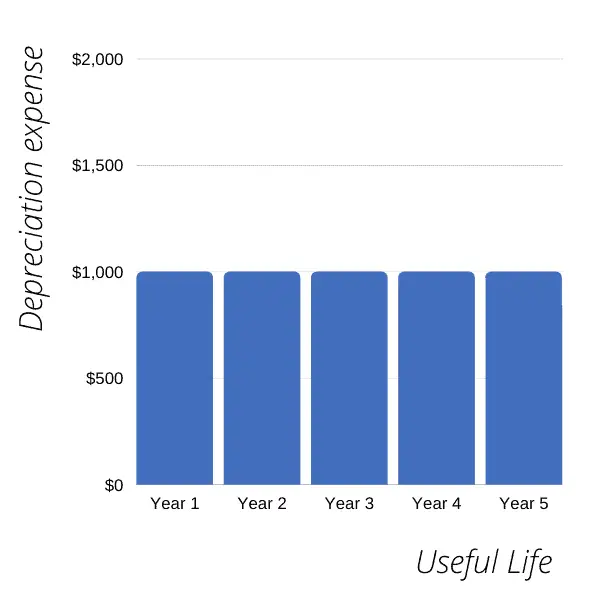
Notice that this graph shows the depreciation expense over an asset’s useful life and not the accounting years, which are rarely the same.
The graph of depreciation expense calculated using the straight line method will always look like the one above if the asset’s useful life coincides with the accounting year.
However, because the assets are usually purchased and sold sometime during an accounting year rather than on the first and last days, the straight line depreciation expense in the first accounting year and the last accounting year is usually lower.
For example, suppose an asset having a depreciable cost of $5000 and a useful life of 5 years is purchased in the middle of an accounting year. In that case, the amount of depreciation expense in the first accounting year will be half of the full year’s depreciation charge.
Plotting the depreciation expense of such asset over the accounting years that fall within its useful life would look something like this on a graph:
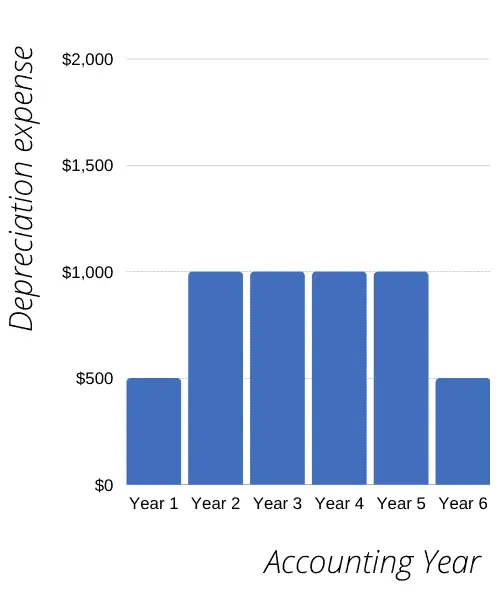
Don’t worry if you’re wondering how each year’s depreciation charge was calculated above.
The following sections will guide you through each step involved in calculating the straight line depreciation for each year of an asset’s life. Make sure to read the example below and solve the quiz towards the end!
Straight Line Depreciation Formula

How to Calculate Depreciation Expense
First-Year Depreciation
First-year depreciation = Annual depreciation × Time Factor
Depreciation expense in the year of acquiring an asset is the full year’s depreciation expense calculated using the straight line depreciation formula and multiplying that by the time factor.
Time Factor is the number of months of the first accounting year that the asset was available to a business divided by 12.
So if the asset was acquired on the first day of the accounting year, the time factor would be 12/12 because it has been available for the entirety of the first accounting year. If an asset is purchased halfway into an accounting year, the time factor will be 6/12 and so on.
Middle Years Depreciation
All accounting years other than the first and the last one are charged depreciation expense in full using the straight line depreciation formula above.
Final Year Depreciation
Final Year Depreciation = Annual Depreciation × Time Factor
The last accounting year in which an asset is depreciated is either the one in which it is sold or the one in which its useful life expires.
Like the first accounting year, the depreciation expense recorded in the last year also needs to be adjusted by the time factor to ensure that the asset is not depreciated above its depreciable cost or after its sale.
For example, if an asset’s useful life ends on the last day of the ninth month, the time factor 9/12 will be used. Likewise, if an asset is sold on the last day of the eleventh month of an accounting year, a time factor of 11/12 will be used.
Example 1

Bill bought a car for his business on 1 October 2020.
The car cost Bill $10,000 and has an estimated useful life of 5 years, at the end of which it will have a resale value of $4000.
Suppose Bill prepares his financial statements on 31 December.
What is the amount of depreciation expense and net book value to be recorded in each accounting year using the straight-line method?
The first thing we need to calculate is the annual depreciation charge using the straight line method formula:
[$10,000 (Cost) MINUS $4000 (Salvage Value)] Divided by 5 (Useful Life in Years) which works out to $1200 per annum.
Using this amount, we can calculate the depreciation expense, accumulated depreciation, and carrying value of the asset for each year as follows. In case you’re confused at any step, read the explanation below the depreciation schedule.
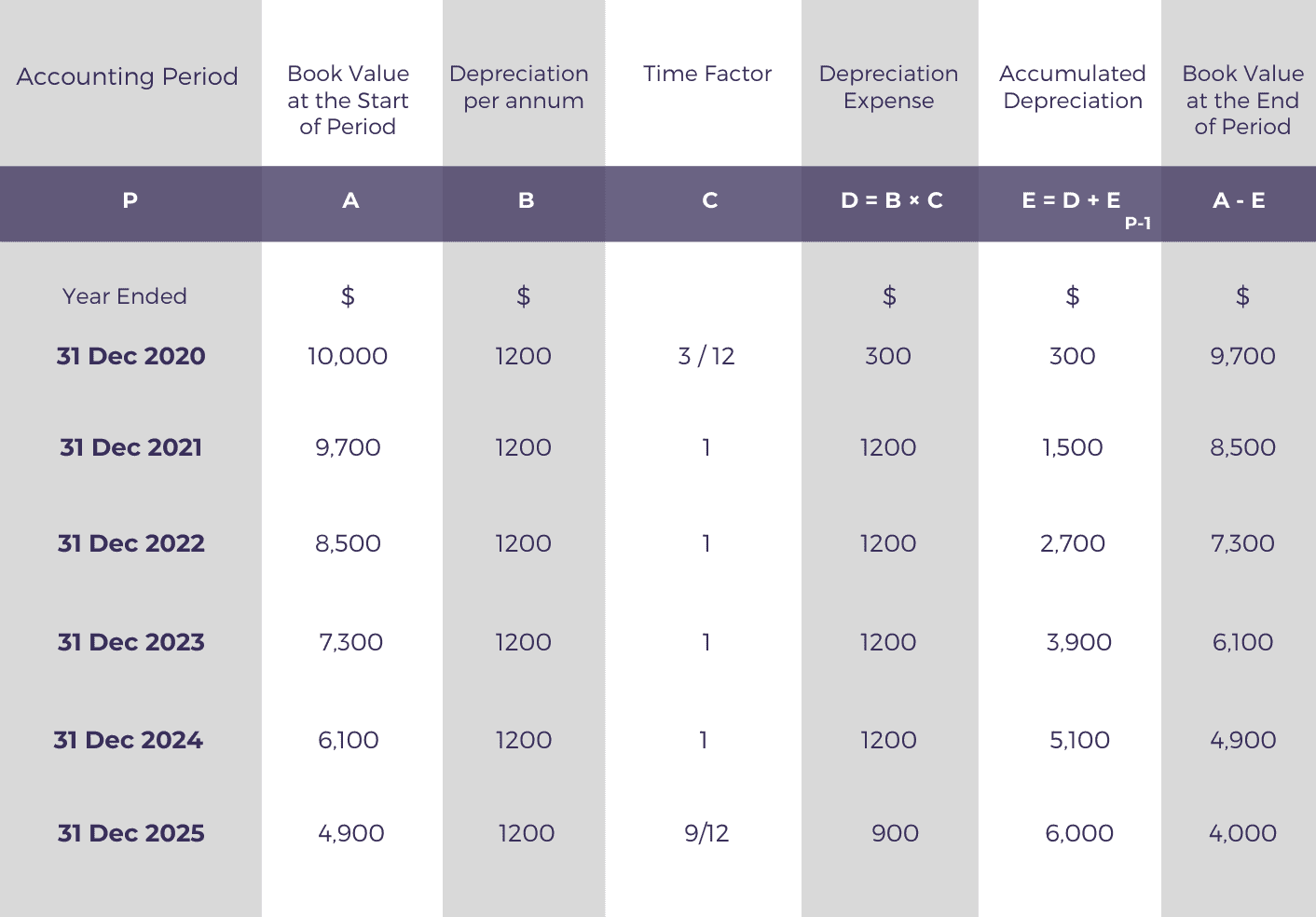
The depreciation expense is charged in full in all accounting years other than the first and the last accounting year.
In the first accounting year, the asset is available only for 3 months, so we need to restrict the depreciation charge to only 3/12 of the annual expense.
Similarly, in the last accounting year, we need to reduce the depreciation expense to just 9 months because the asset will complete its useful life at the end of the ninth month of the year 2025. Beyond this point, no further depreciation will be charged.
Quiz
How much do you know about Straight Line Depreciation?

Question 1
The amount of depreciation expense decreases in each year of an asset’s useful life under the straight line method.
True
Incorrect.
False
Spot on!
Question 2
The straight line method charges the same amount of depreciation in every accounting period that falls within an asset’s useful life.
True
Incorrect.
False
Correct!
Depreciation expense in the first and last accounting periods is usually lower than the middle years because assets are rarely acquired on the first day of an accounting year.
Question 3
If an asset is depreciated at a straight line rate of 20% per annum, what is its useful life?
2 years
Incorrect.
5 years
Correct!
100 divided by 20% is 5.
10 years
Incorrect.
20 years
Incorrect.
Question 4
What is the annual depreciation expense using the straight line method of an asset with a useful life of 36 months that costs $4000 and has a residual value of $400?
$100
Incorrect.
$1000
Incorrect.
$1200
You're right!
($4000 - $400) ÷ 3 = $1200 per annum.
36 months are equal to 3 years of useful life (36 divided by 12).
$1467
Incorrect.
Question 5
What is the useful life of an asset with a cost of $7000, salvage value of $2000, and depreciation of $1000 per annum on a straight line basis?
5 Years
Correct!
Deducting the cost of an asset from its salvage value gives us its depreciable amount which in this case is $5000. Dividing it by the annual depreciation expense ($1000) gives us the useful life in years.
7 years
Incorrect.
10 years
Incorrect.
Question 6
The useful life of an asset ends on 31 December 2022.
What is the accumulated depreciation calculated on 30 June 2020 using the straight line method if the asset was purchased on 1 January 2018 for $12,000 and has a salvage value of $2000?
$1000
Incorrect.
$2000
Incorrect.
$4000
Incorrect.
$5000
You're right!
The asset will accumulate 2.5 years of depreciation out of its total useful life of 5 years. We can simply multiply the annual depreciation amount by 2.5 to calculate the accumulated depreciation.
Annual depreciation expense is equal to ($12000 - $2000) / 5 = $2000.
Accumulated depreciation on 30 June 2020 will therefore be $2000 x 2.5 which is equal to $5000.
$6000
Incorrect.
Illustration provided by Icons8.
How many questions did you answer correctly?
Score Grade
6 Master
5 Pro
4 Pass