Accelerated depreciation techniques charge a higher amount of depreciation in the earlier years of an asset’s life. One way of accelerating the depreciation expense is the double decline depreciation method.
In this lesson, I explain what this method is, how you can calculate the rate of double-declining depreciation, and the easiest way to calculate the depreciation expense.
Double Declining Depreciation
Double declining balance depreciation is an accelerated depreciation method that charges twice the rate of straight-line deprecation on the asset’s carrying value at the start of each accounting period.
For example, if an asset has a useful life of 10 years (i.e., Straight-line rate of 10%), the depreciation rate of 20% would be charged on its carrying value.
Unlike the straight-line method, the double-declining method depreciates a higher portion of the asset’s cost in the early years and reduces the amount of expense charged in later years.
Therefore, it is more suited to depreciating assets with a higher degree of wear and tear, usage, or loss of value earlier in their lives.
Formula
The formula for calculating the rate of depreciation is:
Annual Depreciation % = (2 × 100 ÷ Useful Life in Years)%
Although the depreciation rate under the double-declining depreciation is two times the depreciation rate under the straight-line method, the amount of depreciation expense charged under the straight-line basis is not its exact half.
This is because, unlike the straight-line method, the depreciation expense under the double-declining method is not charged evenly over the asset’s useful life.
The following section explains the step-by-step process for calculating the depreciation expense in the first year, mid-years, and the asset’s final year.
How to calculate Depreciation
First-Year Depreciation
First-year depreciation = Cost × Depreciation% × Time Factor
First-year depreciation expense is calculated by multiplying the asset’s full cost by the annual rate of depreciation and time factor.
It is important to note that we apply the depreciation rate on the full cost rather than the depreciable cost (cost minus salvage value).
Another thing to remember while calculating the depreciation expense for the first year is the time factor.
In the accounting period in which an asset is acquired, the depreciation expense calculation needs to account for the fact that the asset has been available only for a part of the period (partial year).
If, for example, an asset is purchased on 1 December and the financial statements are prepared on 31 December, the depreciation expense should only be charged for one month.
We can incorporate this adjustment using the time factor, which is the number of months the asset is available in an accounting period divided by 12. In the case above, the time factor will be 1/12.
Middle Years Depreciation
Middle Years Depreciation = Carrying Value × Depreciation% × 1
After the first year, we apply the depreciation rate to the carrying value (cost minus accumulated depreciation) of the asset at the start of the period.
Since the assets will be used throughout the year, there is no need to reduce the depreciation expense, which is why we use a time factor of 1 in the depreciation schedule (see example below).
An exception to this rule is when an asset is disposed before its final year of its useful life, i.e. in one of its middle years. In that case, we will charge depreciation only for the time the asset was still in use (partial year). Like in the first year calculation, we will use a time factor for the number of months the asset was in use but multiply it by its carrying value at the start of the period instead of its cost.
Depreciation in the year of disposal if the asset is sold before its final year of useful life is therefore equal to Carrying Value × Depreciation% × Time Factor. No depreciation is charged following the year in which the asset is sold.
Final Year Depreciation
Final Year Depreciation = Carrying Value – Salvage Value
In the last year of an asset’s useful life, we make the asset’s net book value equal to its salvage or residual value. This is to ensure that we do not depreciate an asset below the amount we can recover by selling it.
For example, if an asset has a salvage value of $8000 and is valued in the books at $10,000 at the start of its last accounting year. In the final year, the asset will be further depreciated by $2000, ignoring the rate of depreciation.
After the final year of an asset’s life, no depreciation is charged even if the asset remains unsold unless the estimated useful life is revised.
Example

On 1 October 2020, Sara purchased a laptop costing $2000 for her fashion illustration business.
Sara intends to use the laptop for four years, after which the laptop will have an estimated resale value of $200.
Sara wants to know the amounts of depreciation expense and asset value she needs to show in her financial statements prepared on 31 December each year if the double-declining method is used.
You can assume the laptop is not sold at the end of its useful life.
Here’s the depreciation schedule for calculating the double-declining depreciation expense and the asset’s net book value for each accounting period. In case of any confusion, you can refer to the step by step explanation of the process below.
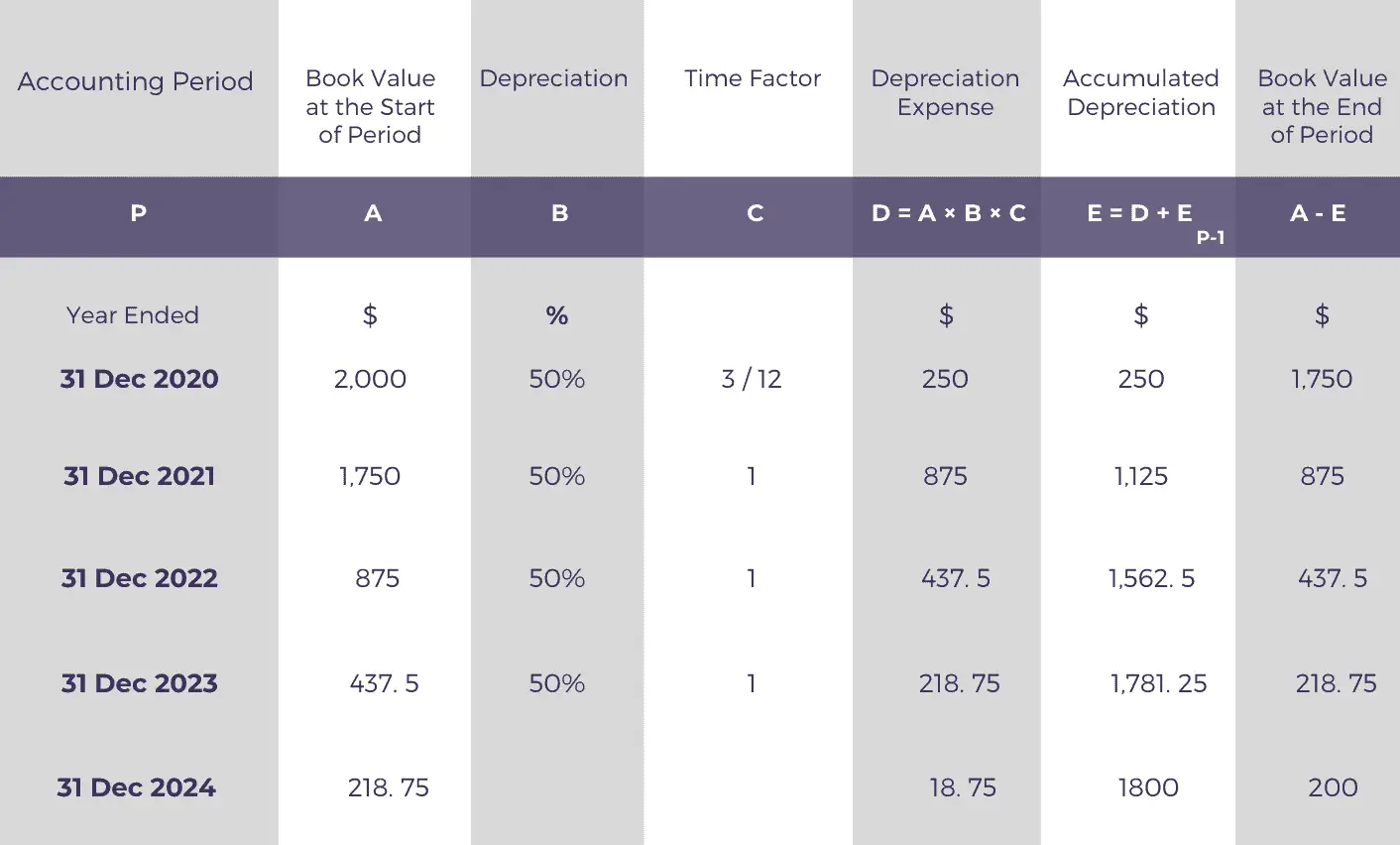
To calculate the double-declining depreciation expense for Sara, we first need to figure out the depreciation rate.
Depreciation % = (2 × 100 ÷ 4)% = 50%
In the first year, we will only charge the depreciation expense for the three months that the laptop was available for use (from 1 October 2020 to 31 December 2020).
To calculate the depreciation expense for the first year, we need to apply the rate of depreciation (50%) to the cost of the asset ($2000) and multiply the answer with the time factor (3/12).
To calculate the depreciation expense of subsequent periods, we need to apply the depreciation rate to the laptop’s carrying value at the start of each accounting period of its life.
For example, the depreciation expense for the second accounting year will be calculated by multiplying the depreciation rate (50%) by the carrying value of $1750 at the start of the year, times the time factor of 1.
The time factor for any accounting period that falls between the first and the last period is 1 because the asset will be available for the entire period and, therefore, should be charged the depreciation expense in full.
The amount of final year depreciation will equal the difference between the book value of the laptop at the start of the accounting period ($218.75) and the asset’s salvage value ($200).
Quiz
How much do you know about the double declining Depreciation?
Instructions for solving quiz:
- Click on one of the given options that you think is correct.
- If you are not sure about a question, review the lesson above.
- Mark yourself out of 6 by rewarding 1 mark for each correct answer.
Good luck!
Question 1
Double-declining depreciation charges lesser depreciation in the later years of an asset’s life.
True
Spot on!
False
Incorrect.
Question 2
The carrying value of an asset decreases more quickly in its earlier years under the straight line depreciation compared to the double-declining method.
True
Wrong.
False
That's correct!
Question 3
Which of the following graphs best illustrates the pattern of depreciation expense charged under the double-declining method over an asset’s useful life?
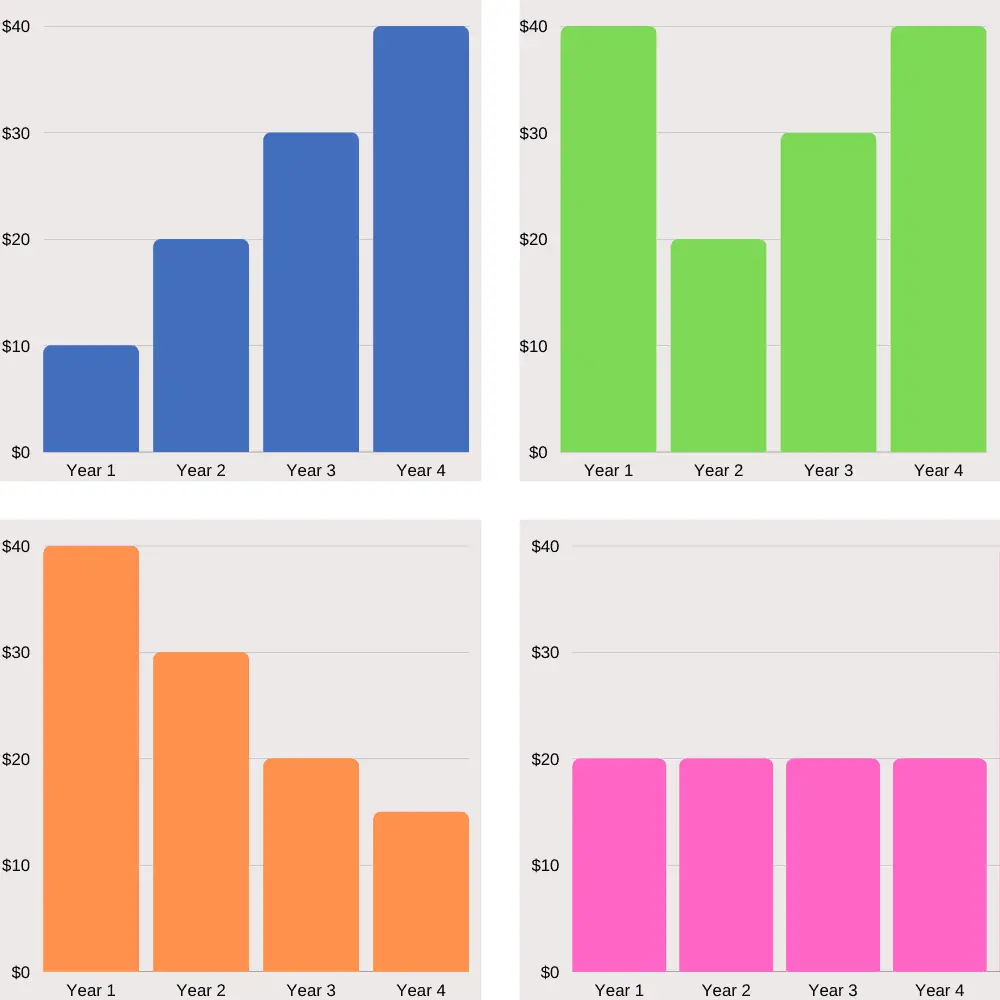
Blue
Incorrect.
Green
Incorrect.
Orange
You're right!
Pink
Incorrect.
Question 4
What is the depreciation rate under the double-declining balance method for an asset with a useful life of 4 years?
50%
You're right!
(2 x 100 / 4)% = 50%
25%
Incorrect.
12.5%
Incorrect.
Question 5
If an asset is depreciated at the rate of 40% using the double decline method, what is the asset’s estimated useful life?
10 years
Incorrect.
5 years
That's correct!
If the double-declining depreciation rate is 40%, the straight-line rate of depreciation shall be its half, i.e., 20%.
Dividing 100% by 20% gives us the estimated useful life of 5 years.
4 years
Not correct.
2.5 years
Wrong answer.
Question 6
An asset costing $6000 is acquired on 1 January 2020. It has a salvage value of $1000 at the end of its useful life of 5 years.
What is the depreciation expense to be charged for the year ended 31 December 2021 calculated on the basis of the double-declining method?
$2000
Not correct.
$1200
Wrong answer.
$1440
That's correct!
Rate of depreciation is 40% (2 x 100 / 5).
Carrying value at the end of the first year will be $3600 ($6000 - $6000 x 0.4).
Depreciation expense for the year 2021 will therefore equal $1440 ($3600 x 0.4).
Residual value will be ignored.
$2400
Incorrect.
Illustration provided by Icons8.
How many questions did you answer correctly?
Score Grade
6 Master
5 Pro
4 Pass